Abstract

The aim of this project is to understand models of quantum geometry that are related to so called BPS states, which arise in supersymmetric gauge theories and string theory. The project focuses on an intricate and interdisciplinary web of dualities involving quantum geometry, strongly coupled phenomena, mathematical theory of quivers, mathematical knot theory, and statistical models.

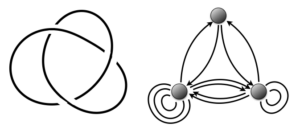
BPS states of a certain supersymmetric three-dimensional theory correspond to generators of HOMFLY homology of trefoil knot (left), and to the nodes of the corresponding quiver (right). The arrows in quiver encode interactions between these BPS states, as well as the structure of corresponding knot invariants.

Team members

• Principal Investigator:

Prof. Piotr Sułkowski

• Postdocs:

Dr Daniel Bryan
Dr Luigi Guerrini

• PhD students:

Pedram Karimi
Jacek Kenig
Souradeep Purkayastha
Abhigyan Saha

About

Since a discovery of Quantum Mechanics around a hundred years ago, we have known that various physical quantities, for example energy, which characterize objects on microscopic scales, are neither continuous nor deterministic. Instead, such quantities take discrete values and obey probabilistic laws. Furthermore, for around a half of the century, we have known the Standard Model – a quantum theory that describes behavior of elementary particles. A new spectacular confirmation of the Standard Model was a detection of the Higgs boson in CERN in 2012. In view of the great success of quantum theory, physicists believe that not only quantities such as energy, but also space and time are quantized, and governed by a hypothetical theory of quantum gravity. A few formulations of quantum gravity have been proposed, however we still have no means to confirm these ideas experimentally. Nonetheless, such ideas are also actively studied in certain simplified models, which are broadly referred to as quantum geometry; not only do they illustrate the essence of interesting physical phenomena, but also inspire and turn out to be deeply related to various branches of contemporary mathematics.

The aim of this project is to understand models of quantum geometry that are related to so called Bogomol’nyi-Prasad-Sommerfield states (referred to shortly as BPS states). BPS states can be thought of as particle-like objects that arise in supersymmetric quantum field theories, i.e. supersymmetric versions of theories similar to the Standard Model. What makes such models even more interesting is that at the same time they enable to illustrate and understand various strongly coupled phenomena, which are too difficult to analyze in Quantum Chromodynamics, i.e. a part of the Standard Model describing strong interactions. In particular, in one class of theories that we are going to study in this project, an infinite family of complicated BPS states arises as bound states of a few basic states, whose interactions are encoded in a graph called a quiver. Moreover, recently the PI with collaborators discovered that for appropriate choices of quivers, at the same time such theories characterize properties of knots (such as those that are tied on a piece of rope), while counting of associated BPS states is captured by combinatorial and statistical models. This leads to an intricate and interdisciplinary web of connections between quantum geometry, strongly coupled phenomena, mathematical theory of quivers, mathematical knot theory, and statistical models. In this project we are going to study such a web of dualities. On one hand, we will reveal properties and calculate various amplitudes in supersymmetric theories, among others by taking advantage of recent developments in mathematical quiver representation theory and knot theory. On the other hand, reinterpreting physical phenomena in mathematical language, we expect to be able to formulate deep mathematical conjectures, which presumably could not be deduced without identifying the above mentioned web of dualities and physical intuition. Above all, we expect that the results of the project will reveal important properties of quantum geometry, and will contribute to formulation of realistic theories of Nature. The project is conducted by the PI and his research group, in the Chair of Quantum Mathematical Physics the PI is also a head of, at the Faculty of Physics, University of Warsaw.

[PL]

Od odkrycia ok. sto lat temu mechaniki kwantowej wiemy, iż różne wielkości fizyczne, np. energia, charakteryzujące mikroskopijne obiekty, nie są ani ciągłe, ani deterministyczne. Wielkości takie przyjmują wartości dyskretne i są opisane probabilistycznymi prawami. Ponadto, od ok. pół wieku znamy Model Standardowy – kwantową teorię opisującą zachowanie cząstek elementarnych. Kolejnym spektakularnym potwierdzeniem Modelu Standardowego była detekcja cząstki Higgsa w CERN-ie w 2012 r. W związku z wielkimi sukcesami teorii kwantów fizycy są przekonani, że nie tylko wielkości takie jak energia, ale też sama przestrzeń i czas mają kwantowy charakter, który opisuje hipotetyczna teoria kwantowej grawitacji. Dotychczas zostało zaproponowanych kilka sformułowań takiej teorii, jednakże wciąż nie jesteśmy w stanie potwierdzić ich eksperymentalnie. Niemniej jednak, idee takie są aktywnie badane w ramach pewnych uproszczonych modeli, określanych zwięźle jako tzw. kwantowa geometria; modele takie nie tylko pozwalają zilustrować istotę interesujących zjawisk fizycznych, ale także inspirują i są ściśle powiązane z różnymi działami matematyki współczesnej.

Celem niniejszego projektu jest zrozumienie modeli kwantowej geometrii, które związane są także z tzw. stanami Bogomol’nyego-Prasada-Sommerfielda (określanymi zwięźle jako stany BPS). O stanach BPS można myśleć jako o mających własności analogiczne do cząstek wzbudzeniach w supersymetrycznych kwantowych teoriach pola, tzn. w supersymetrycznych wersjach teorii podobnych do Modelu Standardowego. Takie modele są szczególnie interesujące, jako że jednocześnie pozwalają one na zrozumienie różnych zagadnień dotyczących zjawisk w reżimie silnego sprzężenia, jak dotąd niemożliwych do analizy np. w ramach chromodynamiki kwantowej, czyli części Modelu Standardowego opisującej oddziaływania silne.  W szczególności, jedna klasa teorii którą zamierzamy zrozumieć w ramach tego projektu, zawiera nieskończoną rodzinę skomplikowanych stanów BPS, które można opisać jako stany związane kilku podstawowych stanów, których oddziaływania opisane są poprzez grafy określane jako kołczany. Ponadto, w ostatnim czasie kierownik niniejszego projektu wraz ze współpracownikami odkrył, iż dla odpowiedniego wybranych kołczanów, teorie takie jednocześnie charakteryzują własności węzłów (takich jakie są wiązane na sznurku), natomiast zliczanie stanów BPS w tych teoriach powiązane jest z modelami kombinatorycznymi i statystycznymi. Zależności te prowadzą zatem do intrygującej, interdyscyplinarnej sieci powiązań (tzw. dualności) między kwantową geometrią, silnie sprzężonymi zjawiskami, matematyczną teorią kołczanów oraz teorią węzłów, jak też modelami statystycznymi. W ramach tego projektu będziemy badać m.in. tę sieć dualności. Z jednej strony, pozwoli to odkryć nowe własności i policzyć pewne amplitudy w supersymetrycznych teoriach, m.in. poprzez odpowiednie przetłumaczenie i wykorzystanie znanych już faktów w matematycznej teorii reprezentacji kołczanów oraz teorii węzłów. Z drugiej strony, interpretacja zjawisk fizycznych w języku matematyki powinna doprowadzić nas do nowych głębokich hipotez matematycznych, które trudno byłoby sformułować bez odwoływania się do intuicji fizycznych. Ponadto, jesteśmy przede wszystkim przekonani, że projekt ten pozwoli na zrozumienie takich własności kwantowej geometrii, które będą istotne dla sformułowania realistycznych teorii opisujących przyrodę. Projekt niniejszy jest prowadzony w grupie naukowej kierownika projektu, działającej w prowadzonej przez niego Katedrze Kwantowej Fizyki Matematycznej na Wydziale Fizyki Uniwersytetu Warszawskiego.

Media

Wywiad z prof. Piotrem Sułkowskim w Radio357

Wywiad z prof. Piotrem Sułkowskim w ramach inicjatywy „Komunikator naukowy”